Геометрия в восьмом классе часто преподносит сюрпризы, и один из первых, с которым сталкиваются школьники — это четырехугольники. Параллелограмм занимает среди них особое место. Представьте себе обычный прямоугольник, который слегка «поехал» в сторону, словно карточный домик под порывом ветра. У него сохранились попарно параллельные стороны, но прямые углы исчезли. Возникает закономерный вопрос: равна ли площадь этой наклонной фигуры площади исходного прямоугольника, или её размер изменился?
Понимание того, как вычисляется занимаемое пространство внутри фигуры, нужно не только для контрольной работы. Это знание пригодится, когда вы решите перестелить пол паркетом, имеющим форму ромбов, или будете раскраивать ткань для сложного дизайнерского изделия. В учебниках встречается множество обозначений, но суть остается неизменной. Мы разберем основные способы вычислений, которые помогут быстро сориентироваться в условиях любой задачи, будь то домашнее задание или реальный ремонт. Главное — понять логику, а не просто зазубрить символы.
Формула через сторону и высоту (Базовая)
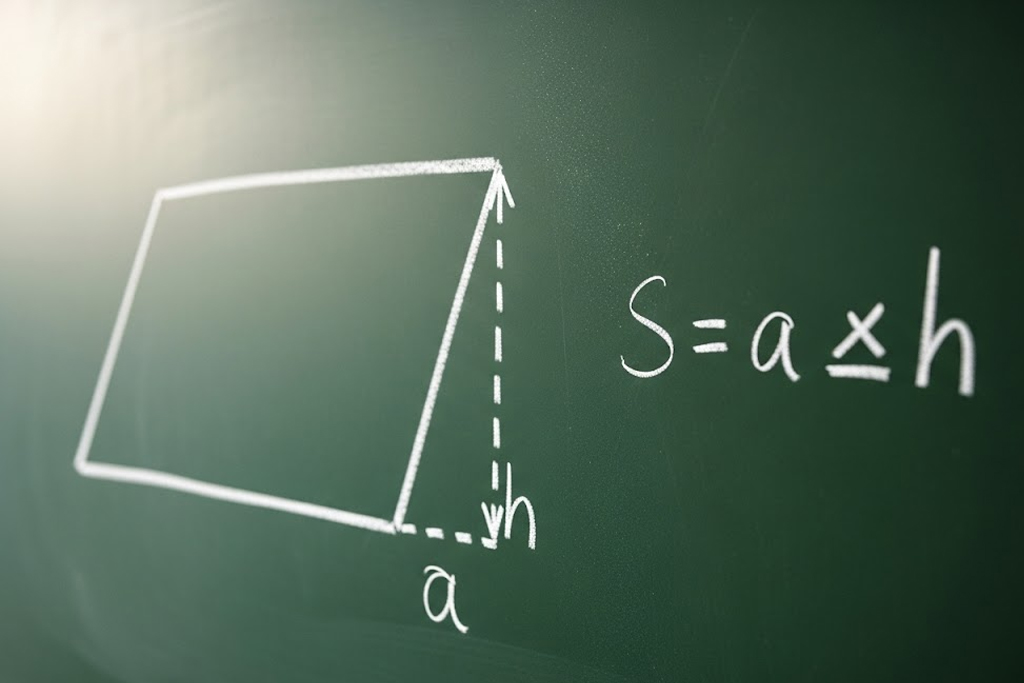
Самый распространенный и интуитивно понятный способ вычисления связан с использованием высоты. Если мысленно отрезать от параллелограмма треугольный «хвостик» с одной стороны и переставить его на другую, фигура чудесным образом превратится в привычный прямоугольник. Именно на этом свойстве базируется классическая формула. Она утверждает, что площадь равна произведению основания на высоту, проведенную к этому основанию. В математической записи это выглядит как S = a · h, где «a» — это сторона, а «h» — высота. Этот метод считается фундаментальным, так как он требует минимум данных и работает безотказно в большинстве стандартных школьных примеров.
Важно помнить, что высота не болтается в воздухе произвольно. Она всегда привязана к конкретной стороне. Если вы умножите высоту на «чужую» сторону (соседнюю, к которой эта высота не проведена), ответ получится неверным. В геометрии точность определений играет решающую роль. Представьте, что вы измеряете высоту комнаты: вы же опускаете рулетку строго вертикально к полу, а не по диагонали к стене. Здесь принцип абсолютно такой же. Этот способ идеально подходит, когда в условии задачи четко прописаны линейные размеры перпендикуляра и стороны, на которую он опирается.
Разберемся подробнее, как не запутаться в чертеже. Часто ученики смотрят на наклонную боковую сторону и ошибочно принимают её за высоту. Чтобы избежать такой оплошности, всегда ищите значок прямого угла на схеме. Именно он сигнализирует о том, что перед вами высота. Использование этой формулы — первый шаг к пониманию того, как найти площадь параллелограмма, зная высоту и основание, не прибегая к сложным тригонометрическим таблицам.
Как определить основание и высоту
Правильное определение компонентов формулы — половина успеха. Основанием может служить абсолютно любая сторона фигуры, не обязательно та, что находится «внизу» на рисунке. Параллелограмм можно крутить как угодно, его площадь от этого не изменится. Основание — это та грань, к которой под углом 90 градусов опускается отрезок из противоположной вершины. Этот перпендикулярный отрезок и называется высотой.
Бывает, что высота падает не на саму сторону, а на её продолжение. Такое случается в фигурах с очень острыми углами. Не пугайтесь, если высота оказалась вне фигуры, за пределами её контура. Для расчетов это не имеет значения: вы все равно умножаете длину самой стороны (без учета продолжения) на длину этого перпендикуляра. Чтобы понять, как найти площадь параллелограмма, зная сторону и высоту, нужно просто визуально или карандашом на чертеже соединить вершину и противоположную линию под прямым углом.
Пример расчета: известна высота и сторона
Рассмотрим конкретную ситуацию, чтобы закрепить теорию. Допустим, перед нами стоит задача: дан параллелограмм, у которого одна из сторон равна 12 сантиметрам, а высота, опущенная именно на эту сторону, составляет 5 сантиметров. Это классический пример, где не нужно ничего достраивать или вычислять дополнительно. Все данные лежат на поверхности, нужно лишь грамотно ими распорядиться.
Берем формулу S = a · h. Вместо «a» подставляем 12, вместо «h» — 5. Перемножаем эти числа: 12 умножить на 5 получается 60. Значит, площадь нашей фигуры составляет 60 квадратных сантиметров. Обратите внимание, что единицы измерения становятся квадратными. Если бы мы взяли другую сторону, например, равную 10 см, то высота, проведенная к ней, была бы другой (в данном случае 6 см), но результат произведения остался бы тем же — 60. Так работает формула площади параллелограмма, принцип нахождения которой теперь стал гораздо понятнее.
Формула через две стороны и угол (Тригонометрическая)
Иногда в задаче нет никаких перпендикуляров, и линейкой их не измерить. Зато известны длины двух соседних сторон и величина угла между ними. В таком случае на помощь приходит тригонометрия. Этот метод спасает, когда построение высоты затруднительно или требует слишком многих дополнительных действий. Формула выглядит так: S = a · b · sin α. Здесь перемножаются две смежные стороны и синус угла, который их соединяет. Этот математический прием позволяет обойтись без построений внутри фигуры.
Суть метода заключается в том, что произведение боковой стороны на синус угла фактически дает нам ту самую высоту, которой не хватало в первой формуле. Математика логична: разные пути ведут к одному результату. Этот способ часто применяется в задачах повышенной сложности или в смежных дисциплинах, например, в физике при расчете векторов. Понимание того, как найти площадь параллелограмма, зная 2 стороны и угол, значительно расширяет ваш инструментарий решения геометрических головоломок.
Для восьмиклассника это может показаться чем-то сложным из-за слова «синус», но на практике все сводится к подстановке числа из таблицы. Вам не нужно вычислять синус самостоятельно, достаточно заглянуть в справочные материалы. Обычно в школьном курсе используются «удобные» углы, значения синусов для которых легко запомнить. Это делает расчет быстрым и элегантным, избавляя от лишних построений с помощью линейки и угольника.
Расчет через синус угла между сторонами
Чтобы воспользоваться этим методом, вам нужно четко идентифицировать две соседние стороны, выходящие из одной вершины. Назовем их «a» и «b». Угол «альфа» должен находиться строго между ними. Если вам дан угол в другой части фигуры, вспомните свойство параллелограмма: сумма углов, прилежащих к одной стороне, равна 180 градусам. А противолежащие углы и вовсе равны. Так что найти нужный градус не составит труда.
Алгоритм действий прост: берем длину первой стороны, умножаем на длину второй, а затем полученное число умножаем на значение синуса угла. Например, если стороны 8 и 10, а синус угла равен 0,8, то расчет будет: 8 · 10 · 0,8 = 64. Этот способ дает ответ на вопрос, как найти площадь параллелограмма через синус, максимально прямолинейно. Главное — не перепутать косинус с синусом в спешке.
Решение задач с углом 30 и 45 градусов
В школьной программе 8 класса обожают углы в 30 и 45 градусов. Они считаются «табличными», и их значения школьники обычно знают наизусть. Синус 30 градусов равен 0,5 (или 1/2). Это настоящий подарок для вычислений: нужно просто перемножить стороны и поделить результат пополам. Рассмотрим, как найти площадь параллелограмма, если известны стороны и угол 30 градусов. Пусть стороны равны 6 см и 8 см. Умножаем 6 на 8, получаем 48. Умножаем на синус 30 градусов (0,5) — получаем 24 квадратных сантиметра.
С углом 45 градусов чуть сложнее в плане арифметики, так как его синус равен корню из двух, деленному на два (≈0,707). Если в задаче стороны заданы целыми числами, ответ часто оставляют с корнем, например, 20√2. Это считается правильной и точной записью. Подобные примеры отлично тренируют навык работы с иррациональными числами. Знание этих нюансов помогает понять, как найти площадь параллелограмма, зная его стороны и угол, даже если числа выглядят пугающе.
Частные случаи: Ромб и Прямоугольник
Геометрия — наука о связях. Ромб и прямоугольник — это родные братья параллелограмма, его частные виды. Поэтому все описанные выше формулы прекрасно работают и для них, но с некоторыми упрощениями. Прямоугольник — это «выпрямленный» параллелограмм. У него угол между сторонами равен 90 градусам. Синус 90 градусов равен единице. Если подставить единицу в тригонометрическую формулу, она превратится в хорошо знакомое S = a · b. То есть произведение длины на ширину. Это подтверждает универсальность математических законов.
Ромб интересен тем, что у него все стороны равны. Если мы используем формулу через высоту, она остается прежней: сторона на высоту. А вот тригонометрическая формула становится красивее: квадрат стороны, умноженный на синус угла (S = a² · sin α). Также для ромба существует уникальная формула через диагонали: половина произведения диагоналей. Но это уже специфическая история именно для ромба. Понимая эти связи, вы легко разберетесь с темой площадь параллелограмма 8 класс.
Встречаются задачи, где фигура описана как «параллелограмм с равными сторонами» (ромб) или «с прямыми углами» (прямоугольник). В таких случаях не нужно искать сложные пути. Используйте свойства этих фигур для упрощения вычислений. Однако помнить общую формулу полезно: она выручит, если вы вдруг забыли частные случаи. Это как универсальный ключ, который подходит к нескольким дверям сразу.
Таблица всех формул площади для 8 класса
Чтобы информация уложилась в голове по полочкам, удобно собрать все методы в одну наглядную схему. В восьмом классе объем формул не так велик, но путаница случается. Ниже представлена сводная таблица, которая поможет быстро освежить память перед контрольной или экзаменом. Здесь собраны основные вариации, которые покрывают 99% школьных задач по этой теме. Особое внимание уделите тому, какие именно данные вам известны: высоты, углы или диагонали (для частных случаев).
| Что дано | Формула | Комментарий |
|---|---|---|
| Основание и высота | S = a · h | Классический метод. Высота h должна падать именно на сторону a. |
| Две стороны и угол | S = a · b · sin α | Используем таблицу синусов. Угол α находится между сторонами a и b. |
| Диагонали и угол (доп.) | S = ½ · d₁ · d₂ · sin φ | Универсальная формула для любого выпуклого четырёхугольника. |
Эта таблица — ваша шпаргалка. Если вы видите в условии сторону и высоту — смотрите первую строку. Видите угол — вторую. Важно помнить, что в разных учебниках буквы могут отличаться, но смысл всегда один. Тема нахождения площади параллелограмма, формула которой может быть записана по-разному, требует лишь внимательности к условиям задачи.
Заключение
Вычисление площади геометрических фигур — это не просто абстрактная гимнастика для ума, а навык видеть структуру в окружающих предметах. Мы разобрали основные инструменты, которые дает геометрия в 8 классе. От простой высоты до использования синусов — каждый метод хорош в свое время. Не бойтесь экспериментировать: попробуйте решить одну и ту же задачу разными способами, если данных достаточно. Это отличная тренировка, которая покажет на практике, как использовать формулу площади параллелограмма из курса геометрии за 8 класс.
Математика любит точность, но она также ценит и понимание сути. Когда вы осознаете, откуда берется формула, вам больше не нужно её зубрить. Мы надеемся, что этот разбор сделал тему прозрачнее и ближе. Если у вас остались вопросы или вы хотите углубиться в другие темы геометрии, рекомендуем прочитать похожие статьи в «Толковке». А ещё, если у вас появилась идея для нового материала или вы заметили неточность — обязательно напишите нам. Редакция читает каждое сообщение и всегда реагирует на обратную связь читателей.